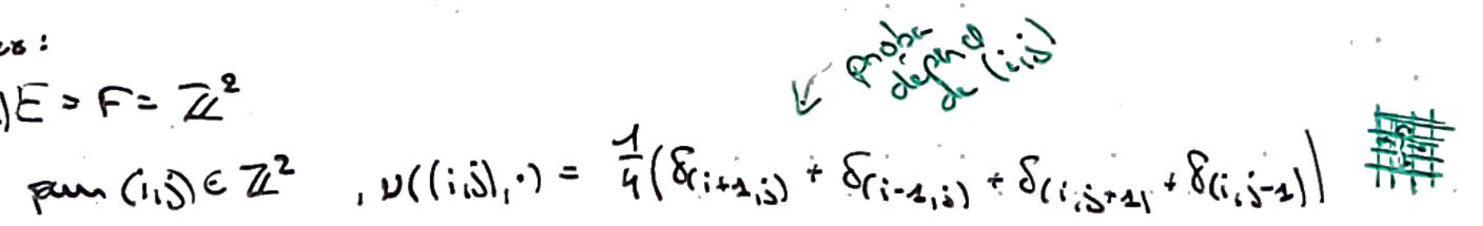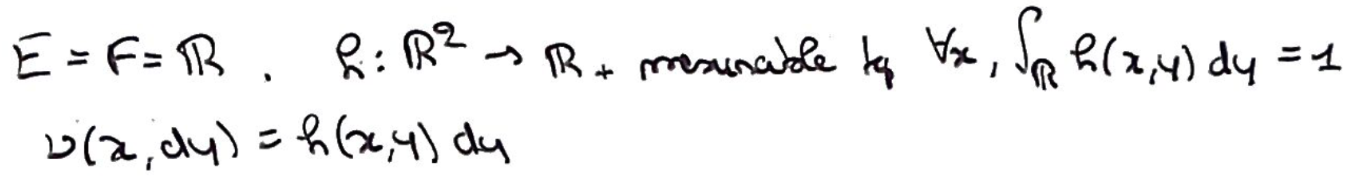Probabilité de transition \(\nu\) de \((E,\mathcal E)\) dans \((F,{\mathcal F})\)
Fonction \(\nu:E\times {\mathcal F}\to[0,1]\) qui est mesurable sur sa première variable et qui est une Mesure de probabilité sur sa deuxième variable. $$\begin{align}\forall x\in E,\quad &A\mapsto \nu(x,A)\text{ est une probabilité sur }(F,{\mathcal F})\\ \forall A\in{\mathcal F},\quad&x\mapsto\nu(x,A)\text{ est }\mathcal E\text{-mesurable}\end{align}$$

• si \(\gamma\) est une mesure de probabilité sur \(E\) et qu'on pose \(\mu(A)=\) \(\int_E\gamma(dx)\nu(x,A)\), alors \(\mu\) est une mesure de probabilité sur \(F\)
• si \(h\) est mesurable et positive/bornée, alors \(x\in F\mapsto\int_{[0,+\infty]}\nu(x,dy)h(y)\) est mesurable et positive/bornée

Questions de cours

START
Ω Basique (+inversé optionnel)
Recto: Donner un exemple de probabilité de transition discrète.
Verso:

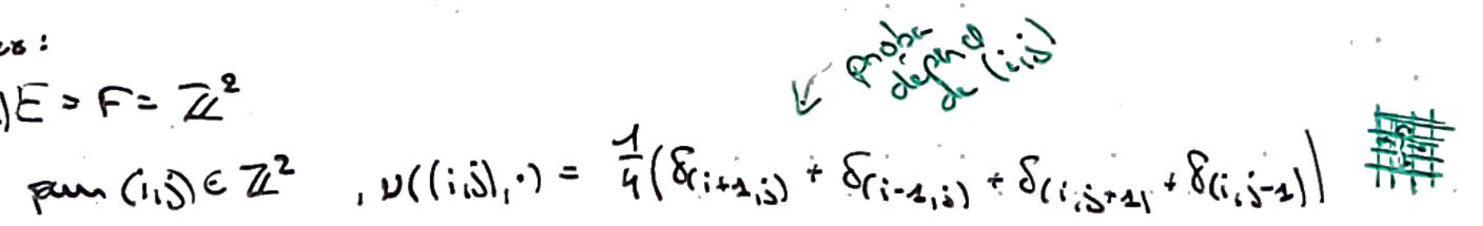
Bonus:
Carte inversée ?:
END
START
Ω Basique (+inversé optionnel)
Recto: Donner un exemple de probabilité de transition continue.
Verso:

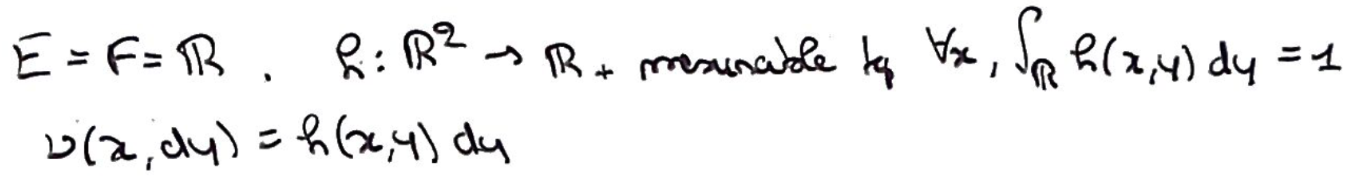
Bonus:
Carte inversée ?:
END

Démontrer 1) :

On a la \(\sigma\)-additivité par \(\sigma\)-additivité de \(\nu(c,\cdot)\).

On vérifie que la mesure globale est bien \(1\) pour \(A=F\).

Démontrer 2) :

(si \(h\) est mesurable et positive/bornée, alors \(x\in F\mapsto\int_{[0,+\infty]}\nu(x,dy)h(y)\) est mesurable et positive/bornée)

Ok pour indicatrice \(\to\) ok pour les étagées par linéarité \(\to\) ok globalement par TCM

START
Ω Basique (+inversé optionnel)
Recto: Que représente une probabilité de transition \(K(Z,A)\) ?
Verso: C'est la mesure de probabilité correspondant ) la Loi conditionnelle sachant \(Z\).
Bonus:

Carte inversée ?:
END

Exercices

On va déjà le montrer pour les indicatrices.

L'espérance conditionnelle relative se traduit alors par la probabilité que \((X,Y)\in A_1\times A_2\) sachant \(Z\).

On peut représenter cela par la Probabilité de transition.

L'hypothèse de l'énoncé nous permettent de conclure pour les indicatrices.

On généralise ensuite le résultat par linéarité et par Théorème de convergence monotone.